Algebra, a fundamental branch of mathematics, plays a pivotal role in various academic disciplines and real-world applications. Its importance is underscored by its prevalence in math exams, where it often carries significant weight. Mastering algebra is essential for proficient problem-solving, particularly in the art of creating and manipulating equations. Among the diverse algebraic techniques, expanding expressions is a crucial skill. This guide will specifically delve into the expansion of perfect squares, offering a step-by-step approach to unravel the intricacies of this process.
Expanding in mathematics refers to the process of removing brackets within expressions. Three common types of expansion include cases where a number or a letter is outside a bracket, double brackets or triple brackets, and perfect squares. This guide will focus on the expansion of perfect squares, where the binomial expression resembles the form (a + b)^2.
To successfully expand a perfect square, follow these three steps:
Step 1: Square the first term Begin by squaring the first term within the bracket. If the expression is in the form (a + b)^2, square the ‘a’ term to obtain ‘a^2’.
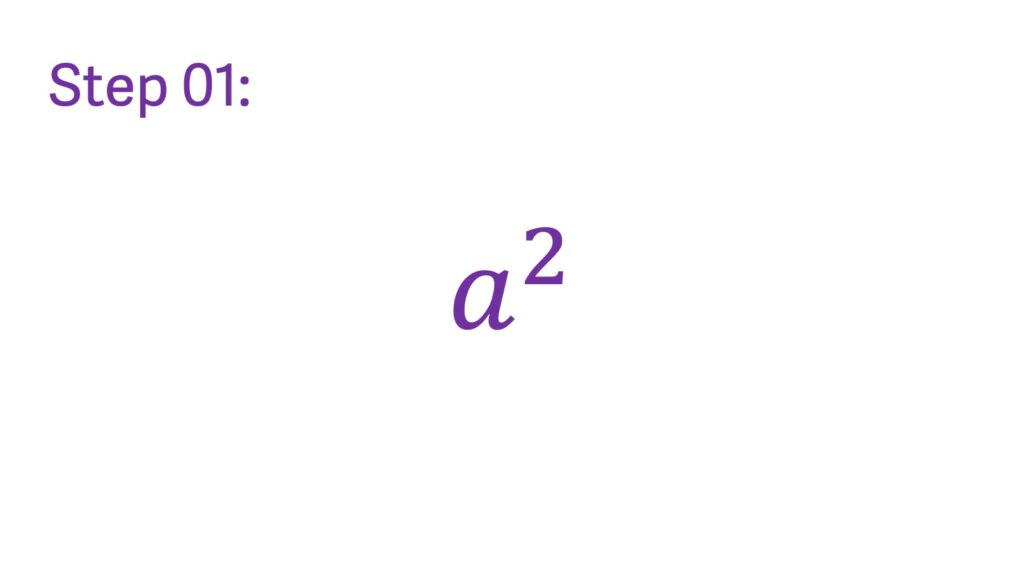
Step 2: Find the product of the square, first term, and second term Calculate the product of the squared first term, the first term, and the second term. This involves multiplying the numbers and letters together. If the expression is (a + b)^2, the product is 2ab.
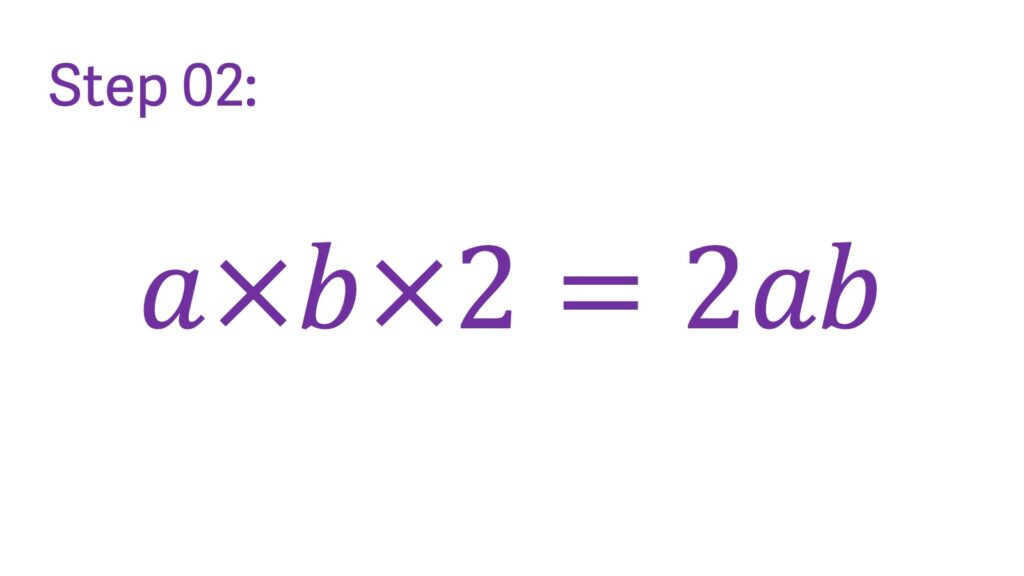
Step 3: Square the last term Square the last term within the bracket. For (a + b)^2, square the ‘b’ term to get ‘b^2’.
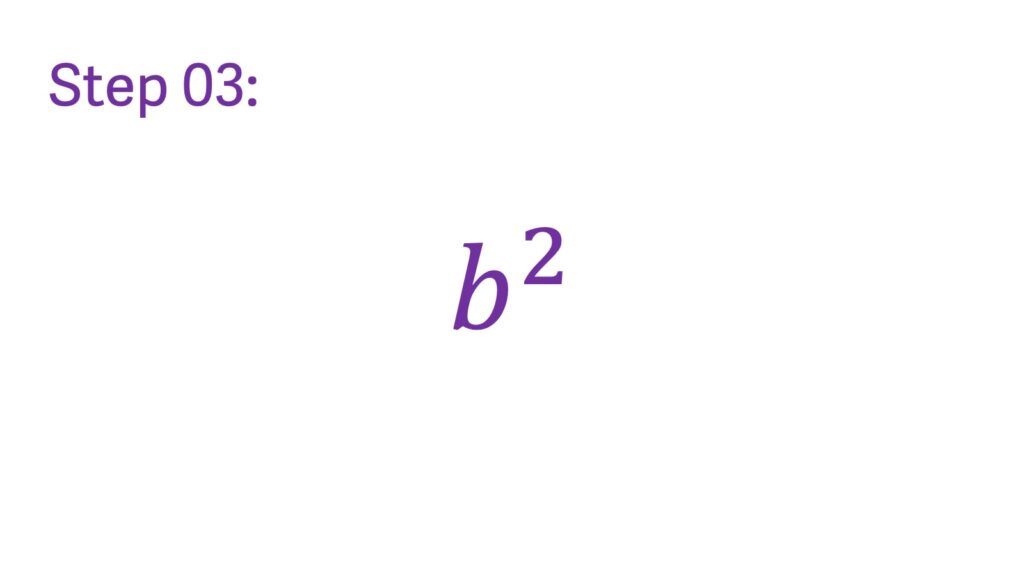
Combine all three terms obtained from the steps above: ‘a^2 + 2ab + b^2’. This is the expanded form of the perfect square.
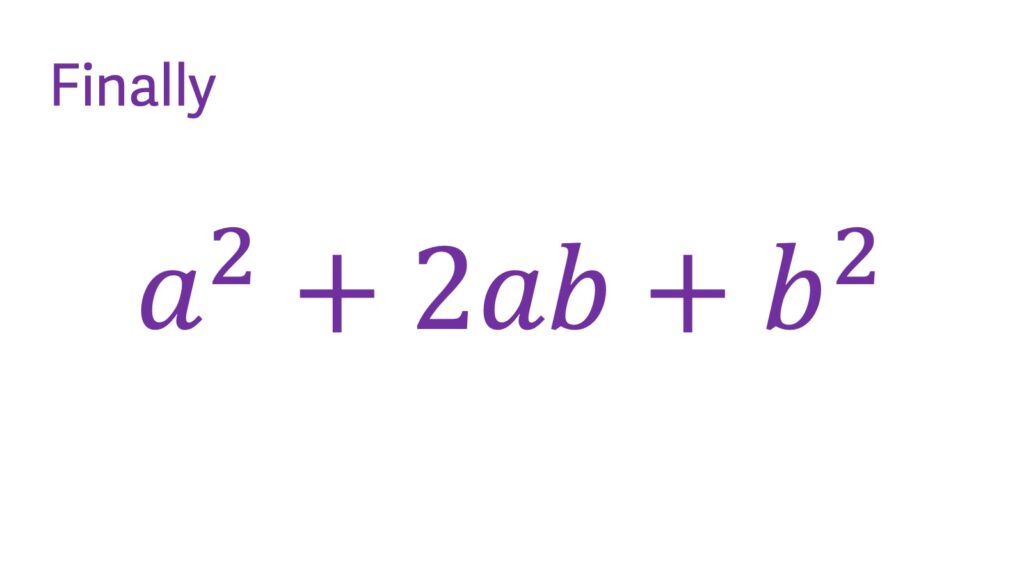
In conclusion, mastering the expansion of perfect squares is a vital skill in algebra. By understanding and applying the three steps outlined in this guide—squaring the first term, finding the product, and squaring the last term—one can efficiently expand perfect squares. This technique is not only crucial for acing algebraic problem-solving but also forms the foundation for more advanced mathematical concepts. As you navigate the world of algebra, remember that a solid grasp of perfect square expansion is a powerful tool in your mathematical toolkit.
